Diffusion

이것은 Diffusion Model에 대한 설명입니다.

Generative Model

생성 모델(Generative Model)은 데이터의 분포를 학습하므로써 해당 분포과 유사한 데이터를 생성하는 모델이다.
데이터 분포에서 log likelihood가 최대화되는 부분에서 sample를 추출하므로써 유사한 데이터를 생성하는 구조이다.

Generative Example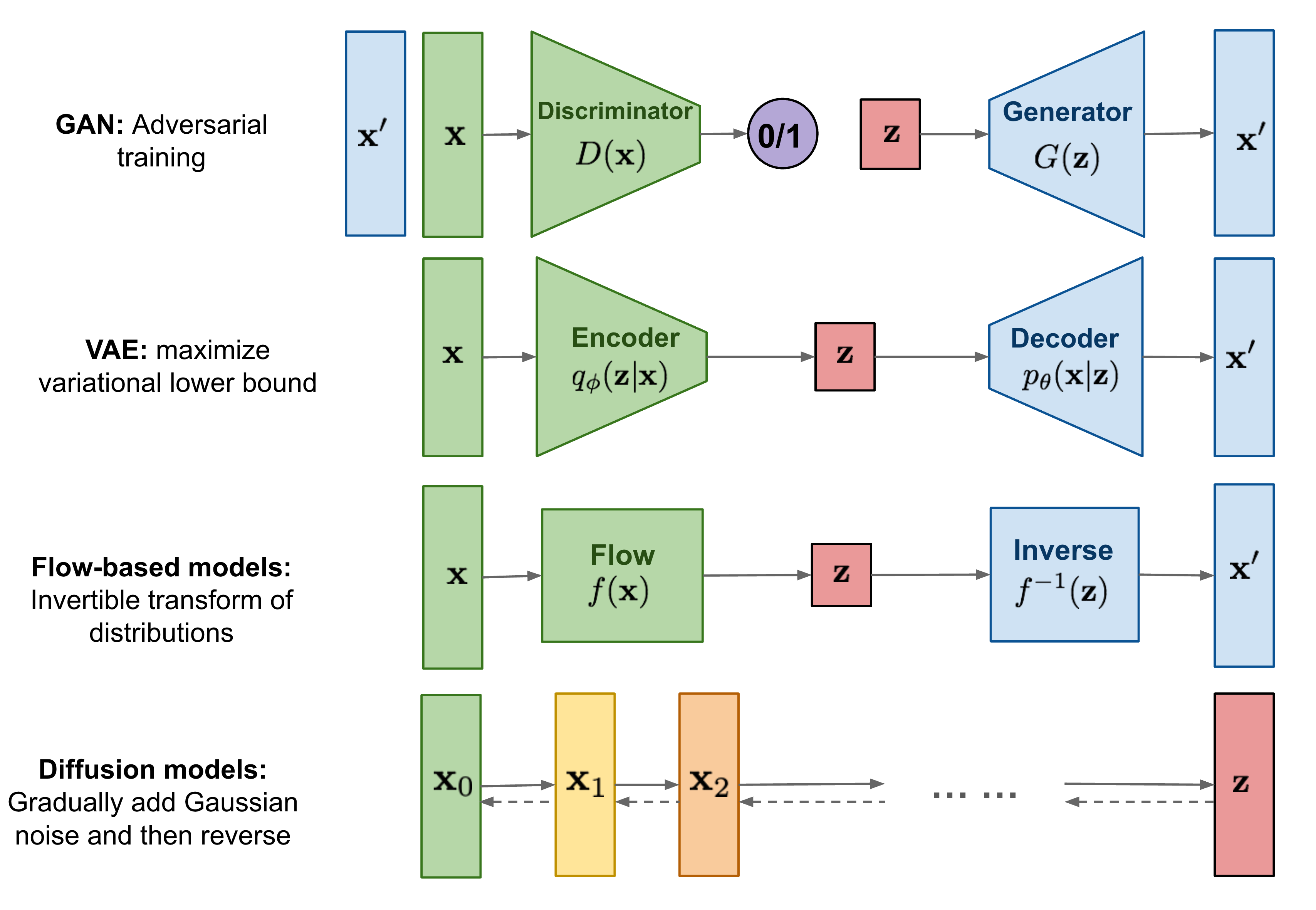

Generative Model
- 생성모델의 대표적인 4가지를 설명한 그림이다.
  - GAN(Generative Adversarial Networks) : 생성자(Generative Model)는 noise(z)로부터 가짜이미지를 생성하면, 판별자(Descriminator)가 진짜와 가짜를 판단한다. 이렇게 두 네트워크는 적대적인 방식으로 서로를 개선하면서 학습한다.
  - VAE(Variational Auto-Encoder) : Encoder를 통해 입력데이터의 특성을 파악한 latent vector z를 만든 후에 z를 통해서 원본 데이터과 유사한 데이터를 생성한다.
  - Flow-based models : VAE과 유사하지만, Encoder가 역함수(inverse)가 존재하는 function의 합성함수로 Encoder로 정의하고, Decoder에서 함성함수의 역함수로 정의한 방식이다.
  - Diffusion models : 데이터에 점진적으로 noise를 추가하고, noise만 남은 데이터를 바탕으로 다시 복원하면서 원본 데이터과 유사한 데이터를 생성한다

Diffusion model

Data에 noise를 조금씩 더하거나 noise로부터 복원해가는 과정을 통해 데이터를 생성하는 모델

Diffusion

Diffusion Model
- Diffusion Model은 DDPM, CFG, LDM로 나뉜다.

DDPM

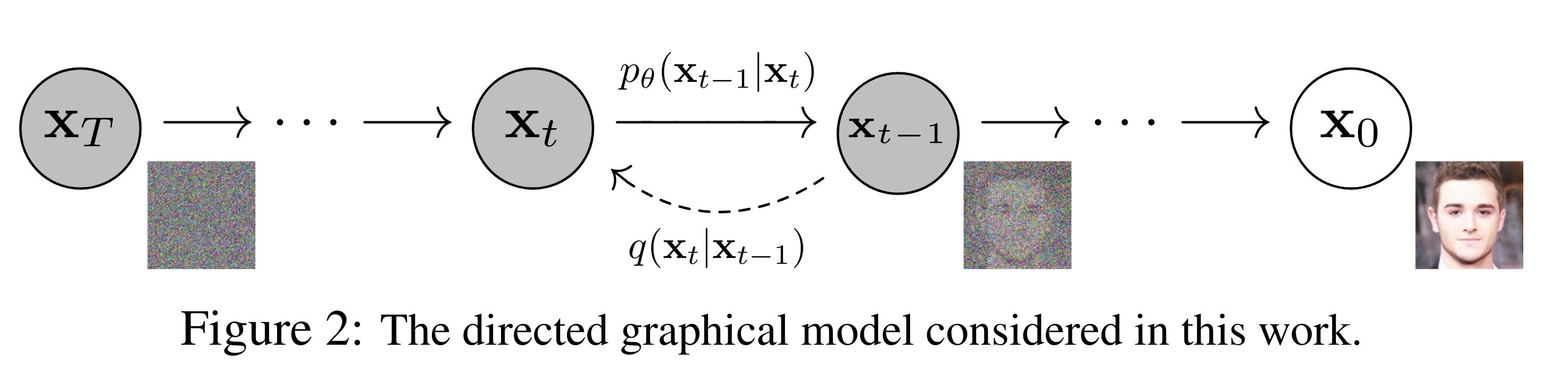
DDPM은 noise를 점점 추가해가는 forward prcess과 noise로부터 복원해나가는 reverse process로 나눈다.

DDPM

Forward Process(diffusion process)

Forward Process
- Foward Process는 원본데이터($x_{0}$)로부터 Gaussian Noise($x_T$)가 될때까지 Gaussian Noise를 추가하는 Markov Process를 의미한다.
- 수식을 설명하면, 현재 시점의 이미지가 주어질 때 다음 시점의 이미지는 평균이 $$sqrt(1-\beta_{t}), 분산이 \beta_{t}I인 Gaussian의 분포를 따르도록한다.
- $\beta_{t}$는 noise의 variance를 결정하는 파라미터로 얼만큼 noise를 추가할건지를 결정한다. 즉, $\beta$가 1이면 오직 noise만 추가하므로써 한번에 noise($x_t$)가 된다는 의미이다.
- 기존 Diffusion Model은 Forward Process에서 $\beta$를 학습하는것이 목적이다.
- 그러나 DDPM에서는 $\beta$를 1e-4 ~ 0.02로 linear하게 증가시켜서 부여하는 방식으로 사용한다. -> 학습을 하지 않고 고정된 상수값만 사용(고정해도 성능이 잘 나올 뿐 아니라 계산량을 줄일 수 있음)
- $x_t$를 구하기 위해서 원본데이터로부터 t시점까지 forward process를 t번 수행하는 것은 매우 비효율적 -> 수식을 정리하여 한번에 수행 가능
Forward Process
```
  self.beta = self.prepare_noise_schedule().to(device)
  self.alpha = 1. - self.beta
  self.alpha_hat = torch.cumprod(self.alpha, dim=0)

  def prepare_noise_schedule(self):
      return torch.linspace(self.beta_start, self.beta_end, self.noise_steps)

  def noise_images(self, x, t):
      sqrt_alpha_hat = torch.sqrt(self.alpha_hat[t])[:, None, None, None]
      sqrt_one_minus_alpha_hat = torch.sqrt(1 - self.alpha_hat[t])[:, None, None, None]
      Ɛ = torch.randn_like(x)
      return sqrt_alpha_hat * x + sqrt_one_minus_alpha_hat * Ɛ, Ɛ
```
Reverse Process(diffusion process)

Reverse Process

Forward Process
- Reverse Process는 noise($x_{t}$)만 있는 데이터에서 noise를 점점 제거하면서 원본 데이터로 복원하는 과정이다.
- 기존 Diffusion Model은 가우시안분포를 학습하는 것이 목적이기 때문에 mean과 variance를 학습하는 것이 목적이다.
- 그러나 DDPM에서는 variance대신에 beta를 활용한다.(mean만 학습에 사용) -> $p(x_{t-1} \lvert x_{t})의 variance가 \beta$에 영향을 받기 때문에 학습시키지 않는다.

Loss

원본 데이터($x_0$)의 분포를 찾아내는 것이 목적이므로 $p(x_0)$를 maximize해야한다.
그러나, Diffusion model은 실제 데이터의 분포를 모르기 때문에 특정값으로 계산할 수가 없다. -> VLB를 사용
VLB(Variational Lower Bound) : 실제 데이터의 Log Likelihood를 근사하는 값의 lower bound이다.
diffusion model에서는 VLB를 loss function으로 사용한다.

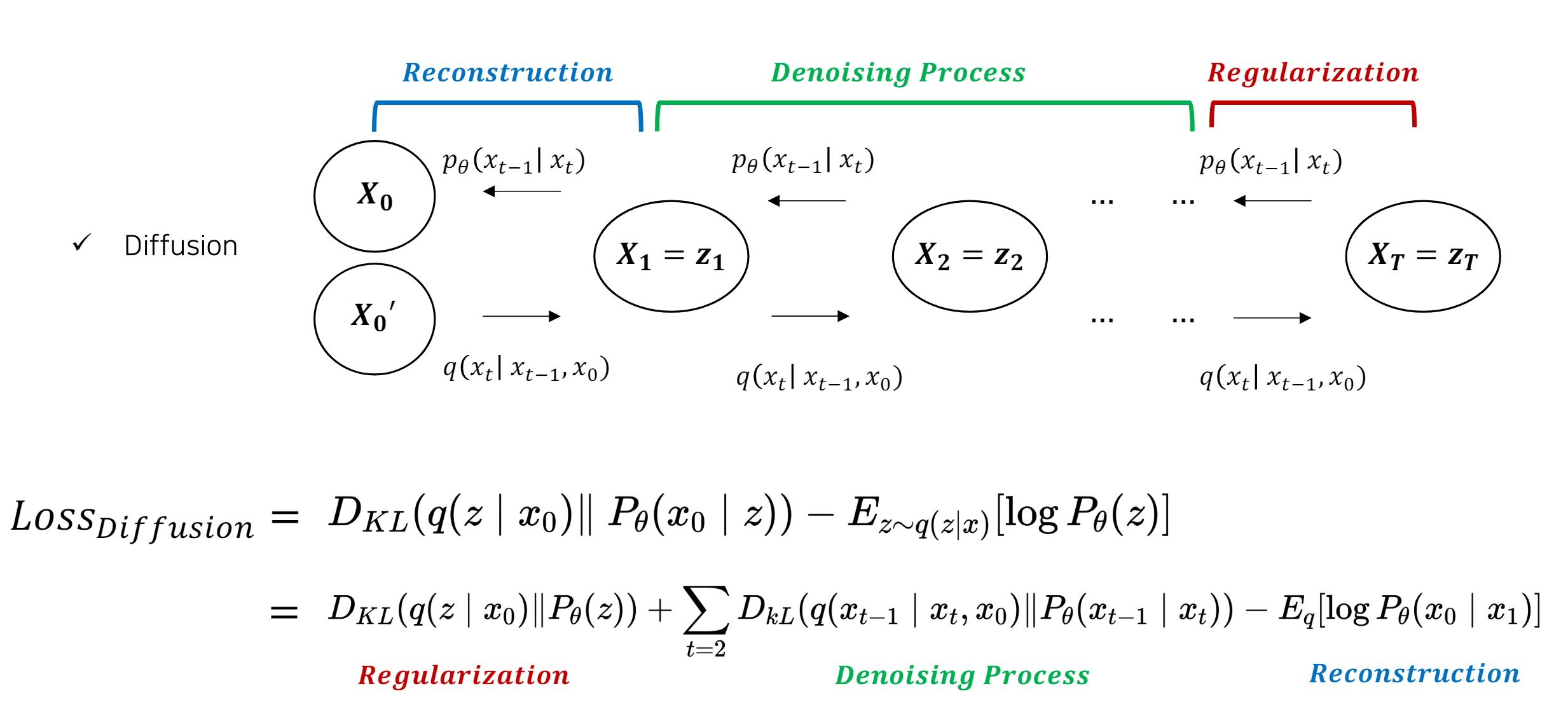
Loss

diffusion model에서 VLB는 3가지 term으로 나눌 수 있다.
- $L_{T}(Regularization)$ : 원본데이터($x_{0}$)가 주어졌을 때 p가 noise($x_{t}$)를 생성하는 가우시안확률분포과 q가 noise($x_{t}$)를 생성하는 가우시안확률분포간의 차이 최소화
  - Forward Process를 수행할 때, 사전에 정의한 Prior p과 유사하도록 q를 설정하므로써 과도한 noise를 추가하지않도록 정규화를 수행한다. -> DDPM에서는 forward process를 학습시키지 않기로 했기 때문에 상수취급
- $L_{0}(Reconstruction)$ : latent vector x1으로부터 $x_0$를 추정하는 확률을 최대화
  - 전체 step중 한번만 계산되기 때문에 비중이 작음. -> DDPM에서는 상수취급
- $L_{t-1}(Denoising Process)$ : p과 q의 가우시안확룰 분포를 최소화.
  - $q(x_{t-1} \lvert x_{t})$는 Bayes Rule로 계산가능(전개식은 생략)

$L_{simple}(\theta)$

diffusion model은 VLB를 사용하는 것은 이해했는데, 실제로 DDPM은 diffusion model를 간소화시키므로써 loss도 간소해진다.

Loss Simple
1. $\beta$를 학습시키지 않으므로 Regularization term를 제외함
2. reverse process에서 variance를 $\beta$로 활용하므로써 denoising process를 재구성함.
  - denoising process를 재구성하는 전개식은 생략함.

=> 결론적으로 우리가 학습하고자하는 파라미터는 $\epsilon$이다. 즉 각 시점의 noise만 예측하면 된다.

DDPM Training

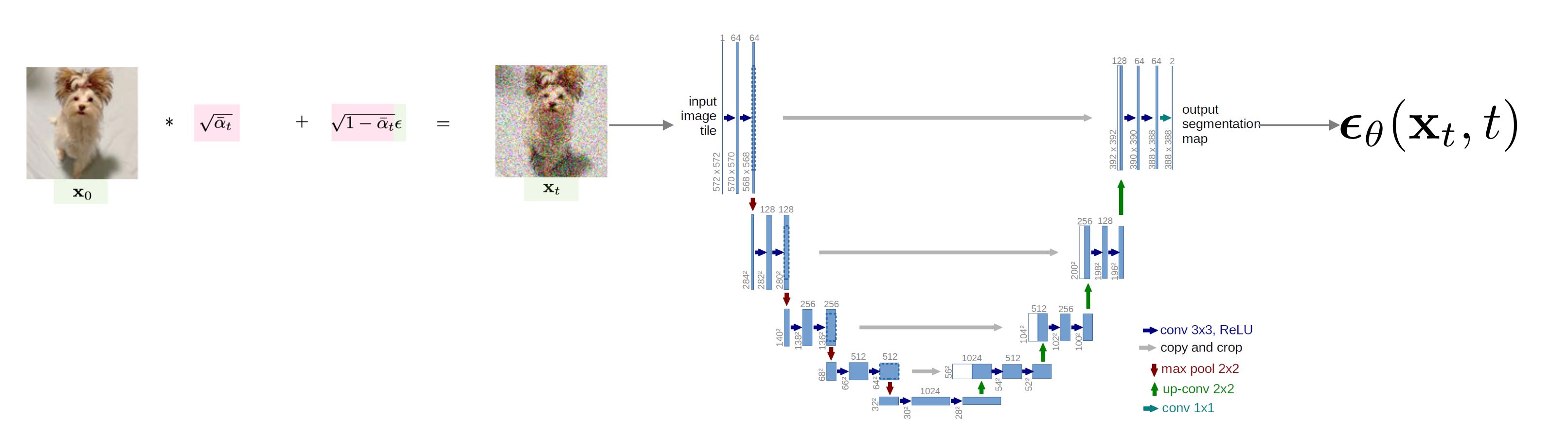
DDPM에서 모델은 U-net를 활용한다.

U-net은 image segementation에서 다루는 딥러닝 모델로 U자 형태의 구조를 가진다. 이는 encoding단계에서 채널의 수를 늘리면서 차원을 축소해 나가고, decoding단계에서 다시 채널의 수를 줄이고 차원을 늘려서 고차원의 이미지로 복원하는 구조를 갖는다.

Training & Sampling

Train

DDPM Training

원본데이터를 $x_t$로 만드는데 noise를 예측하는 모델

원본데이터($x_0$)를 불러온다.
noise를 추가할 time step를 랜덤으로 추출함.
Gaussian를 따르는 랜덤한 $\epsilon$를 추출함
현재 시점의 latent vector $x_t$를 계산함.
latent vecotr $x_t$과 time step에 U-net를 거치므로써 noise를 예측함.
$L_{simple}(\theta)$를 통해 gradient descent수행

for epoch in range(args.epochs):
    for i, (images, _) in enumerate(dataloader):
        images = images.to(device)
        t = diffusion.sample_timesteps(images.shape[0]).to(device)
        x_t, noise = diffusion.noise_images(images, t)
        predicted_noise = model(x_t, t)
        loss = mse(noise, predicted_noise)
    
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

Sampling

DDPM Sampling

$x_T$부터 시작함.
각 시점별로 학습한 U-net를 통해 noise를 예측함.
현재 시점의 $x_t$에서 noise만큼을 제거해서 $x_{t-1}$로 복원함
마지막 step의 $x_0$가 우리가 생성한 데이터

  for i in tqdm(reversed(range(1, self.noise_steps)), position=0):
      t = (torch.ones(n) * i).long().to(self.device)
      predicted_noise = model(x, t)
      alpha = self.alpha[t][:, None, None, None]
      alpha_hat = self.alpha_hat[t][:, None, None, None]
      beta = self.beta[t][:, None, None, None]
      if i > 1:
          noise = torch.randn_like(x)
      else:
          noise = torch.zeros_like(x)
      x = 1 / torch.sqrt(alpha) * (x - ((1 - alpha) / (torch.sqrt(1 - alpha_hat))) * predicted_noise) + torch.sqrt(beta) * noise

Latent Diffusion model

<p align="center">   <img src="https://theaisummer.com/static/ecb7a31540b18a8cbd18eedb446b468e/40ffe/diffusion-models.png">   <br>
  DDPM Sampling
</p>

Generative Model

Diffusion model

DDPM

Loss

\(L_{simple}(\theta)\)

DDPM Training

Latent Diffusion model