위 논문은 Neural Information Processing Systems (NeurIPS) 2017에 출판되었는데, 대규모 배치 학습에서 발생하는 일반화 격차(generalization gap)를 줄이기 위한 방법을 제안하며 학습률과 학습 방법을 조정하여 성능을 향상시키는 전략을 연구한다.
Abstract
- 대규모 배치 크기(Large Batch Size)를 사용할 때 generalization performance이 떨어지는 일반화 격차(generalization gap) 문제가 발생하는데, 이를 해결하기 위해 다양한 연구들이 진행되어 왔습니다.
- 본 논문에서는 generalization gap이 충분한 학습이 이루어지지 않았기 때문에 발생한다고 주장한다. 따라서, 학습 체계를 조정하면 이 문제를 해결할 수 있다고 주장한다.
- 특히, 초기에는 높은 학습률(learning rate)을 사용하고, 추후에는 초기 가중치와의 거리를 바탕으로 학습률을 조정함으로써 일반적으로 사용되는 검증 오류(validation error)를 기반으로 한 학습률 조정 방식과는 다른 접근법을 제시한다.
Introduction
- 딥 뉴럴 네트워크(DNN, Deep Neural Network)는 매우 complex하고 non-convex하기 때문에 optimization method로는 주로 SGD(Stochastic Gradient Descent)를 사용한다.
-
SGD를 사용하여 모델의 generalization performance이 높게 나타나는 현상을 설명하는 연구(Understanding deep learning requires rethinking generalization)도 존재한다.
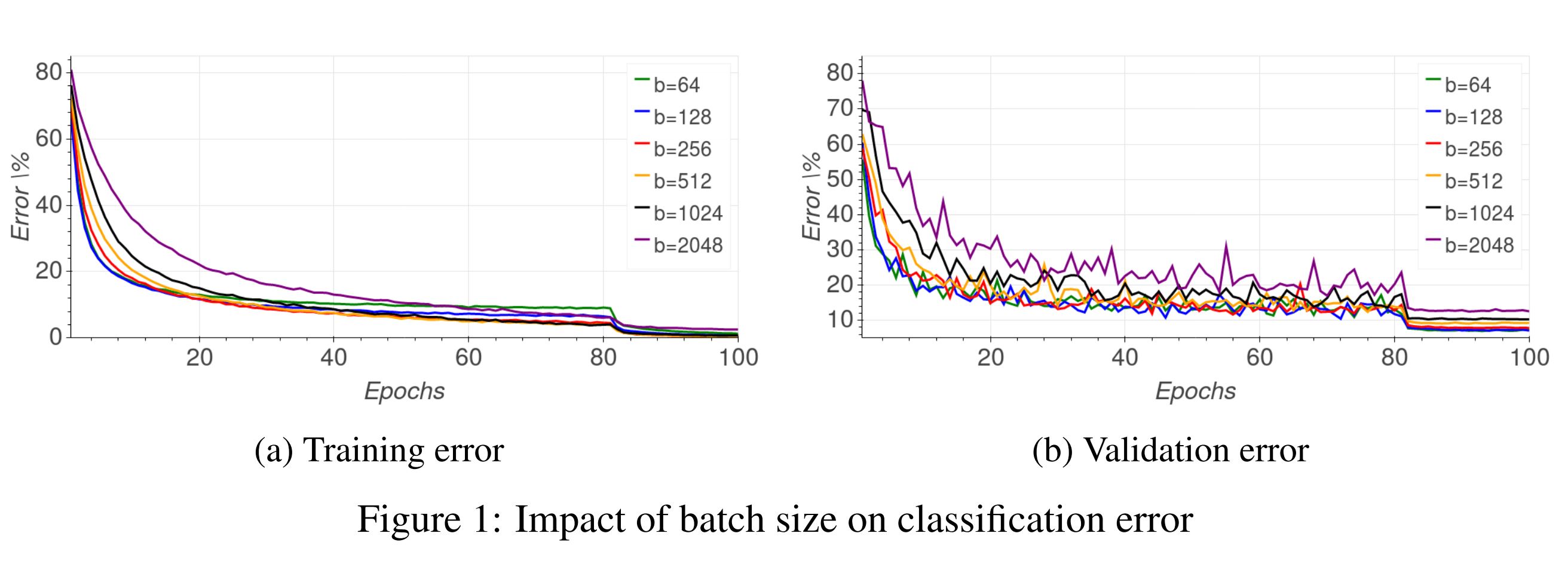
Figure 1: Impact of batch size on classification error- Figure1을 보면 batch size가 크면 클수록 validation error가 증가하고 튀는 것을 확인할 수 있다. 이러한 현상을 우리는 일반화가 잘 되지 않았다고 하며, 일반적으로 batch size가 클수록 이러한 현상이 발생한다.
- 작은 batch size를 사용할 때는 각 배치가 데이터의 일부 샘플만을 사용하여 업데이트되기 때문에 샘플의 다양성에 의한 noise가 발생한다. 그리고 이러한 noise는 모델이 다양한 parameter space를 탐색하도록 하여 더 넓고 평탄한 최소점(flat minima)을 찾을 수 있다. 그러나 큰 batch size를 사용할 경우, 각 배치가 데이터 전체에 대한 평균을 사용하기 때문에 노이즈가 줄어들고 이로 인해 local minima에 빠질 수 있다.
Why Should We Use Large Batch Sizes?
- Parallelize : 병렬 연산 향상
- Learning time : 학습 수렴 속도 향상
- Memory : 메모리와 자원 효율성 향상
Contribution
- 본 논문은 Large Batch Size를 사용할 때 발생하는 generalization gap 문제를 다양한 학습 체계를 활용하여 해결하고자 한다. 저자가 강조하는 핵심 메시지는 다음 문장에 담겨 있다:
- “There is no inherent ‘generalization gap’: large-batch training can generalize as well as small batch training by adapting the number of iterations.”
- 결국, 일반화 격차는 large batch size 자체에서 비롯된 것이 아니며, 충분한 학습 반복 횟수와 학습 체계를 조정하면 해결될 수 있다는 것을 말하고 있다.
- Generalization gap을 해결하기 위해 이 논문에서는 learning rate과 batch normalization를 조정했다. 특히, 일반적으로 사용되는 training or validation errors의 변화에 따른 learning rate 조정 없이, 초기 높은 학습률을 사용했다.
Method
-
증명은 다루지 않으므로 논문을 참고하기를 바란다.
Theoretical Analysis
- SGD(Stochastic Gradient Descent) 기반의 딥러닝 최적화 과정을 수학적으로 설명한 부분이다.
Random Walk on a Random Potential
- 딥러닝에서 optimization 과정을 통계 물리학 관점에서 분석한 내용인데, 이론적인 부분은 모두 알지 못하지만 기본적인 내용만 파악하고 넘어간다.
- 결국 저자가 말하고 싶은 것은 DNN loss surface가 랜덤 워크(불규칙하게 움직이는 입자의 경로를 설명하는 확률적 과정)나 랜덤 포텐셜(입자가 무작위의 힘에 의해 움직이는 환경)처럼 복잡한 형태를 가지고 있다는 것이다.
- 본 논문에서는 딥러닝의 입자 움직임이 “ultra-slow diffusion”이라고 주장한다. 실제로, 입자가 이동한 거리가 다음과 같이 \(\log t\) 형태로 증가한다:
Figure 2: Euclidean distance of weight vector from initialization- Figure2는 학습 시간이 경과함에 따라 초기 가중치 벡터와의 거리를 시각화한 것이다.
- Large-batch size에서는 parameter space를 탐색하기 위해 많은 시간이 소요된다. 또한, learning rate를 조정하면 가중치 벡터와의 거리가 상대적으로 비슷한 패턴을 보임을 확인할 수 있다.(small-batch처럼 다양한 parameter space 탐색이 가능해짐)
Learning rate
- 서로 다른 mini-batch size에서 발생하는 확산 비율(diffusion rate)의 차이를 조정하여 generalization gap를 해결한다.
- mini-batch size에 따라 weight 업데이트의 통계를 일치시키기 위해 공분산 매트릭스를 구한다. 이때, 공분산을 일정하게 유지하기 위해서는 학습률(\(\eta\))이 mini-batch size(\(M\))의 제곱근에 비례해야 함을 발견했다 : \(\eta \propto \sqrt{M}\).
Ghost Batch Normalization
- TabNet 논문에서 소개된 GBN(Ghost Batch Normalization)은 generalization gap을 해결하기 위한 방법 중 하나이다. large batch size가 데이터의 다양성을 제대로 포착하지 못하는 문제를 해결하기 위해, large batch size를 더 작게 나눈 virtual(“ghost”) batch로 분할하고 각 가상 배치마다 정규화를 수행하여 일반화 오류를 줄이는 방식이다.
- 사실 이미 multi-device distributed setting에서 사용되고 있다. 각 디바이스별로 추가적인 communication cost를 피하기 위해서 device별로 batch norm statistics를 계산한다.
Algorithm 1: Ghost Batch Normalization (GBN)- Algorithm1인 GBN 알고리즘에서 언급되는 \(\epsilon\)은 수치적으로 0이 되지 않도록 하는 매우 작은 값(논문에는 언급이 없음)
- 알고리즘이 복잡해 보일 수 있지만, 기본적으로는 mini-batch 단위로 평균과 표준편차를 계산한 후 정규화하는 과정이다.
Ghost Batch Normalization python code- GBN을 구현하는 코드는 간단하다. PyTorch에서 제공하는 Batch Normalization 모듈(torch.nn.BatchNorm1d)을 mini-batch 단위로 적용하면 된다. 이를 자신의 모델에 적용할 때는
b_x = GBN(logit)와 같이 사용하면 된다.
Adapting number of weight updates eliminates generalization gap
- 초기 높은 learning rate를 사용하면 더 넓은 local minima를 탐색할 수 있고 이로 인해 일반화 성능이 향상될 수 있다. (실제로 Figure 2에서도 학습률을 조정함으로써 weight vector 간 거리가 커지는 것을 확인할 수 있다)
-
결론적으로 learning rate를 감소시킬 시점을 결정할 때, validation error가 아닌 weight vector 간의 거리를 활용하는 것이 좋은 기준이 될 수 있다고 주장한다. 즉, validation error가 plateau에 도달해도 높은 learning rate를 계속 사용한다는 것이다.
Figure 3: Comparing generalization of large-batch regimes, adapted to match performance of smallbatch training.- Figure3은 제안된 학습 체계를 적용했을 때, large batch size도 기존의 small batch size처럼 수렴할 수 있음을 보여준다.
weight vector간의 거리를 계산한 python code-
위 코드는 weight vector 간의 거리를 계산하는 코드이다. 따로 threshold을 설정하여 이 값을 넘으면 학습률(learning rate)을 줄이는 방식이 있을 줄 알았지만, 실제로는 log에만 기록되는 것 같다. 즉, 직접 log를 확인하여 특정 epoch를 지나면 learing-rate을 줄이는 방식으로 구현한 것 같다.
-
다만, batch size가 커지면 그에 따라 학습 횟수도 늘려야 한다. 이를 위해 학습 횟수를 다음과 같이 조정해야 한다:
\[\frac{|B_L|}{|B_S|} e \text{ epochs}\] -
예를 들어, 기존에 epoch = 100, batch size = 32로 학습하다가 batch size를 1024로 변경하는 경우 학습 횟수는 다음과 같이 조정된다:
\[100 \times \left(\frac{1024}{32}\right) = 3200 \text{ epochs}\] - Learning rate 역시 batch size를 키우면 함께 증가시켜야 한다. 이는 다양한 parameter space를 탐색할 수 있기 때문이다(Figure2참고) 이를 위해 learning-rate를 다음과 같이 조정해야 한다:
- \[\eta_{L} = \sqrt{\frac{|B_L|}{|B_S|}} \eta_{S}\]
Experiment
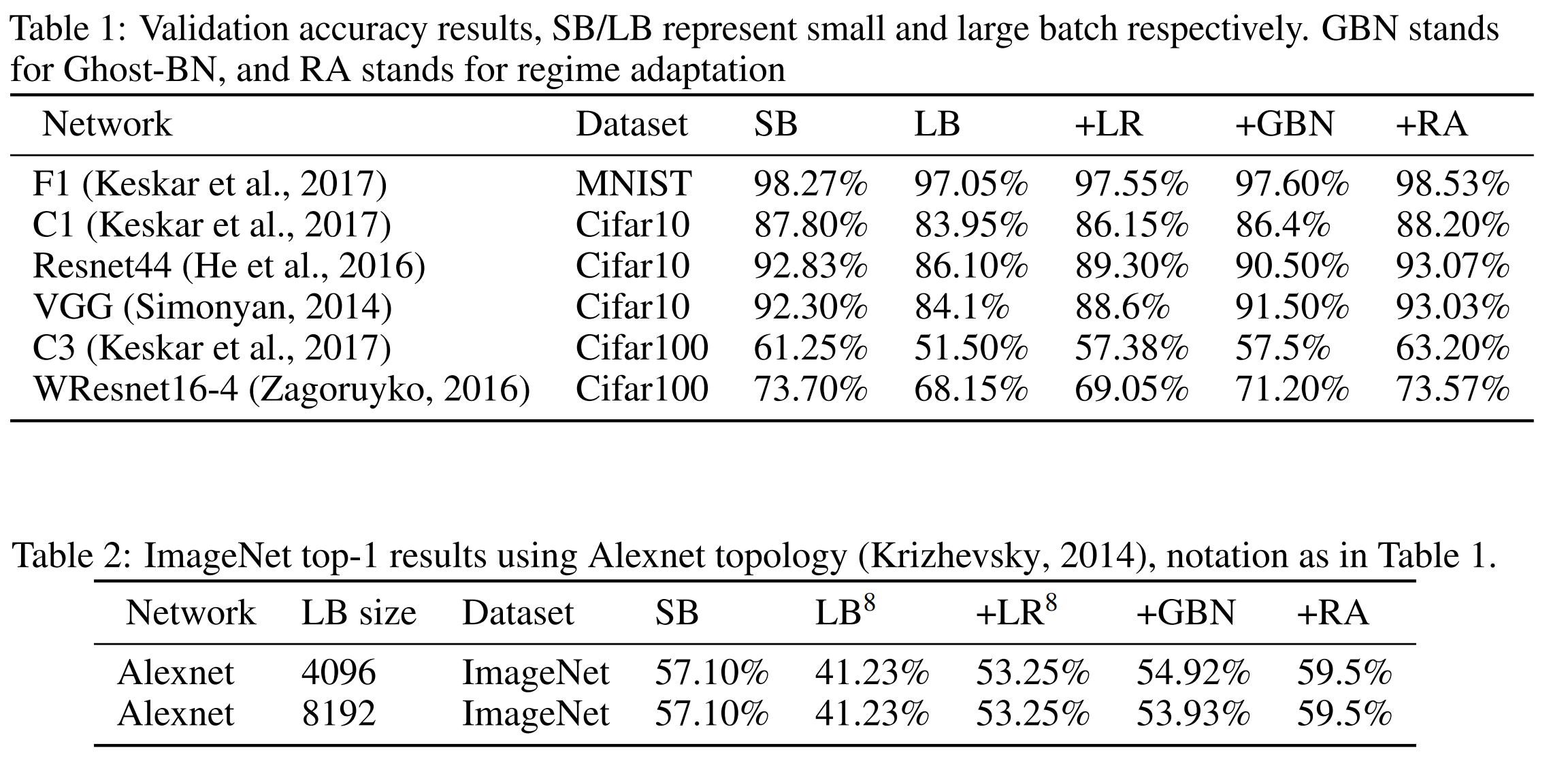
- MINIST, Cifar10, Cifar100, ImageNet등 다양한 데이터셋을 통한 실험 결과이다.
- SB : Small-batch 학습
- LB : Large-batch 학습
- +LR : LB + 학습률 조정
- +GBN : ‘+LR’ + Ghost-BN
-
+RA : ‘+GBN’ + 학습 횟수 조정(Regime Adaptation)
Table 1, 2: Validation accuracy results- Table1 2는 각 기법의 Validation accuracy를 비교한 것이다. SB(Small-batch)가 LB(Large-batch)에 비해 훨씬 성능이 좋은 것을 확인할 수 있으며, 이는 generalization gap 문제를 나타낸다. 그러나, LB에서 제안된 기법들을 적용하면 성능이 개선되어 generalization gap을 극복할 수 있음을 보여준다.
- 특히 CIFAR-100을 사용한 C3 모델의 경우, SB보다도 +RA(Regime Adaptation)를 적용한 학습이 더 높은 성능을 보이는 것이 주목할 만하다.

 Algorithm.JPG)